About

The best way to fluently learn and apply your times tables knowledge is to practise with not just the standard tables questions, but with many different types of question. These could be missing number questions, division, finding fractions of a number, and working with numbers in the tens and hundreds columns, and in the decimals.

KS2 Times Tables does all of this for you, so that each level stretches your memory and speed skills more and more. The app changes the times tables, the operation, and how the questions are written, to cover the arithmetic skills of the KS2 National Curriculum. By the time you pass the Kryptonite tests, you will be fluent and confident enough to use your knowledge of times tables in a huge range of questions.

When you open the app, you choose your level from Bronze to Kryptonite. When you tap the ‘Start’ button you get five minutes to answer forty questions. Only one question appears at a time, to help you concentrate. If you aren't sure what the answer is, make your best guess – there is no ‘Skip’ button! After you finish all 40 questions, or the five minutes run out, you get personal feedback on which kinds of question to focus on, to help you truly know all your times tables back to front and inside out.

Bronze

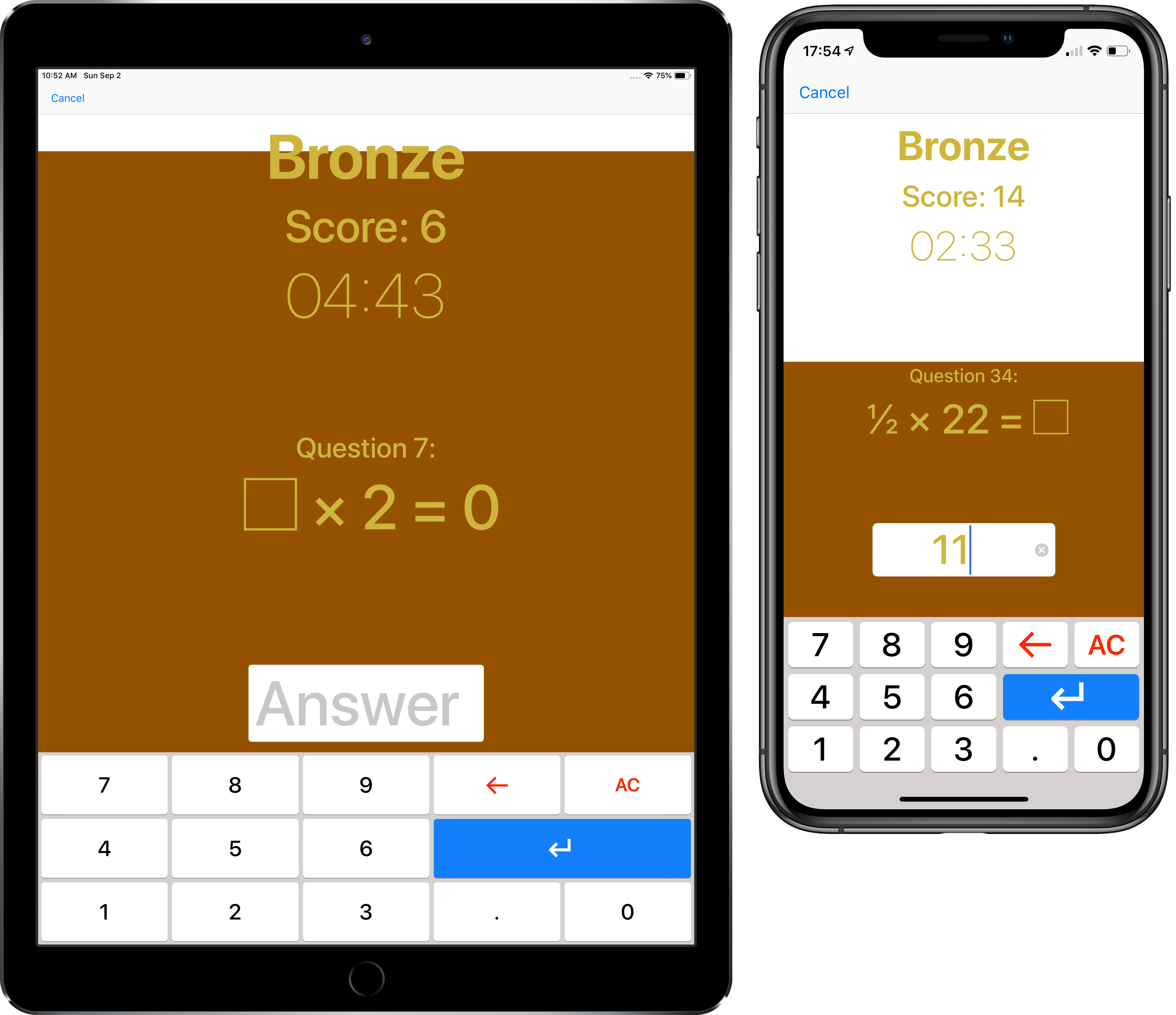
Bronze focusses on the related facts of the 2, 4 and 8 times tables. If you know your two times table, you can use it to help you learn the four and eight times tables, so they're together on one level. You will find questions with 0 up to 12, as sometimes people make mistakes with zero!

Here are the question types you will practise:

• Multiplying 2, 4 or 8 by a number between 0 and 12:
• 4 × 9 = ☐
• Missing number: what do you multiply by 2, 4 or 8 to get the answer?
• ☐ × 8 = 24
• Missing number: 2, 4 or 8 is missing – which do you multiply by to get the answer?
• 9 × ☐ = 18
• Missing number, but with the equals sign at the beginning, learning that the equals sign doesn't just mean “the answer is…”!
• 12 = 4 × ☐
• Dividing by 2, 4 or 8:
• 14 ÷ 2 = ☐
• Dividing by 2, 4 or 8, with the equals sign at the beginning:
• 3 = 24 ÷ ☐
• Finding a half, quarter or eighth of an amount, and learning that ‘×’ means ‘of’:
• ½ × 12 = ☐
• Missing number: the answer is a half, quarter or eighth of which missing number?
• 6 = ¼ of ☐

Silver

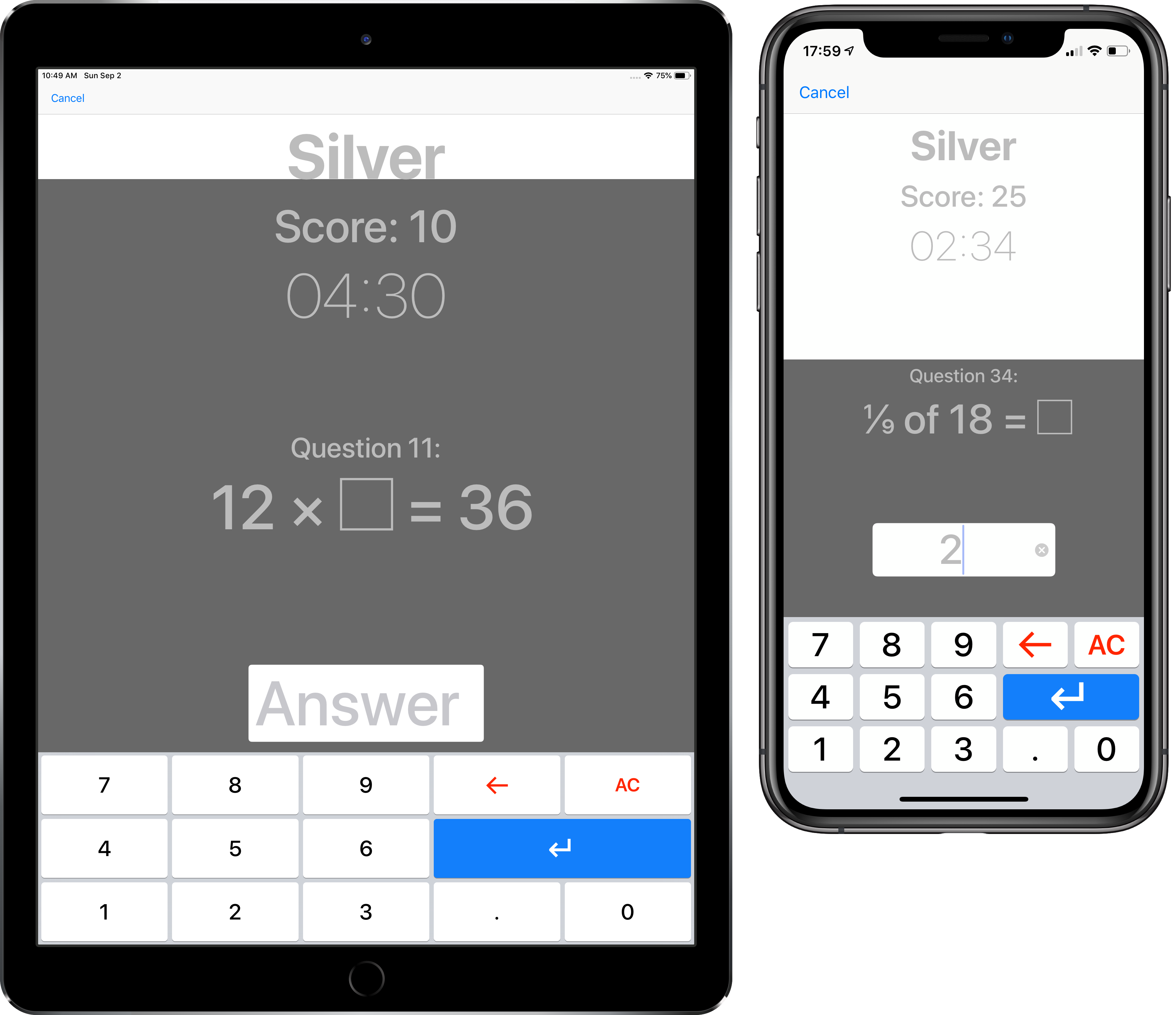
Silver focusses on the related facts of the 3, 6 and 9 times tables. If you know your three times table, you can use it to help you learn the six and nine times tables, so they're together on one level. You will find questions with 0 up to 12, as sometimes people make mistakes with zero!

Here are the question types you will practise:

• Multiplying 3, 6 or 9 by a number between 0 and 12:
• 6 × 11 = ☐
• Missing number: what do you multiply by 3, 6 or 9 to get the answer?
• ☐ × 9 = 36
• Missing number: 3, 6 or 9 is missing – which do you multiply by to get the answer?
• 12 × ☐ = 36
• Missing number, but with the equals sign at the beginning, learning that the equals sign doesn't just mean “the answer is…”!
• 30 = 6 × ☐
• Dividing by 3, 6 or 9:
• 15 ÷ 3 = ☐
• Dividing by 3, 6 or 9, with the equals sign at the beginning:
• 7 = 63 ÷ ☐
• Finding a third, sixth or ninth of an amount, and learning that ‘×’ means ‘of’:
• ⅓ × 30 = ☐
• Missing number: the answer is a third, sixth or ninth of which missing number?
• 11 = ⅙ of ☐

Gold

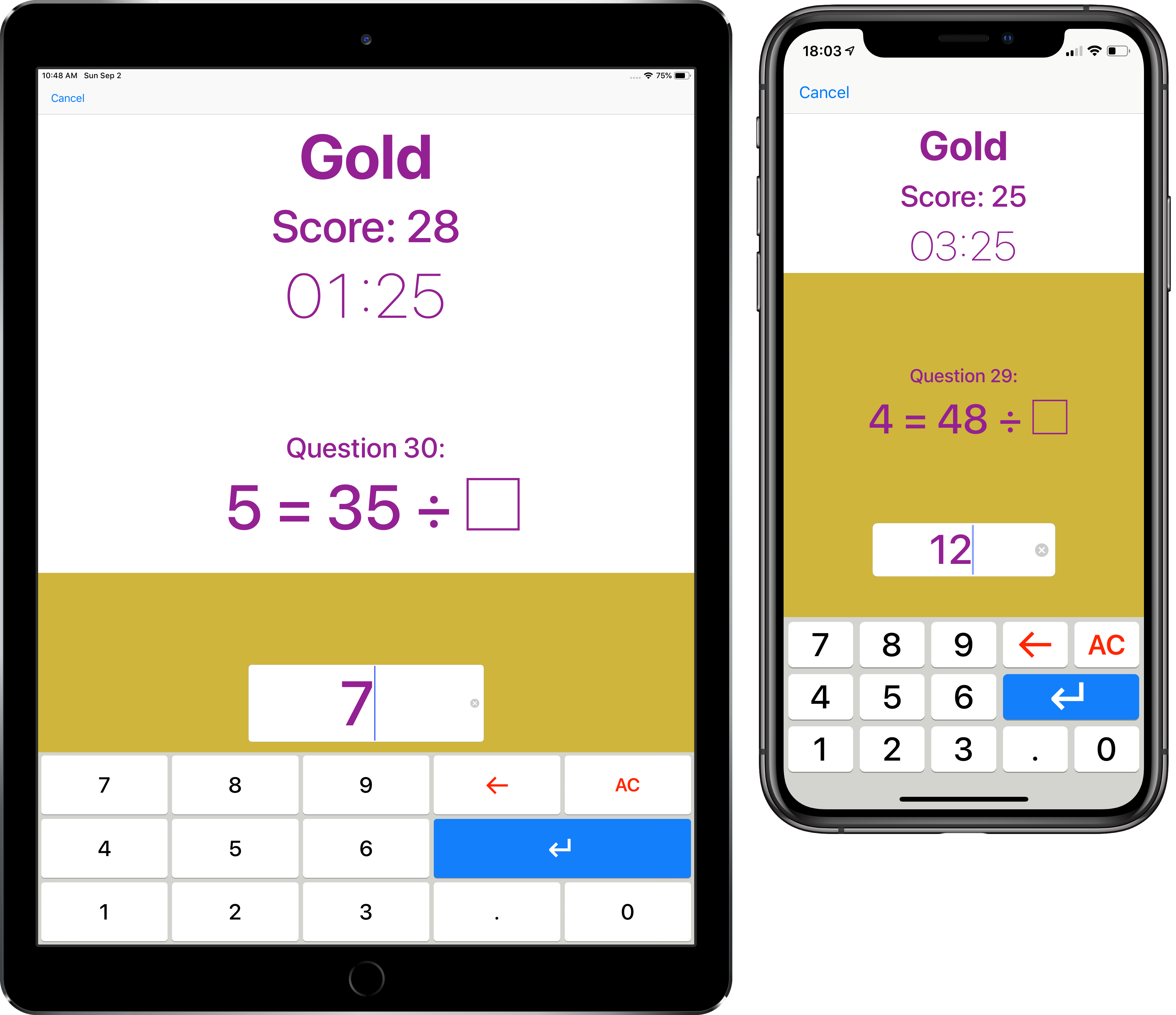
Gold includes all the times tables up to 12. You will find questions with 0 up to 12, as sometimes people make mistakes with zero!

Here are the question types you will practise:

• Multiplying by a number between 0 and 12:
• 7 × 12 = ☐
• Missing number: what do you multiply by to get the answer?
• ☐ × 5 = 0
• Missing number, but with the equals sign at the beginning, learning that the equals sign doesn't just mean “the answer is…”!
• 77 = 7 × ☐
• Dividing by a number from 2 to 12:
• 60 ÷ 5 = ☐
• Dividing with the equals sign at the beginning:
• 5 = 25 ÷ ☐
• Finding a fraction of an amount up to one twelfth, and learning that ‘×’ means ‘of’;
• ⅐ × 84 = ☐
• Missing number: the answer is a fraction of which missing number?
• 10 = ⅕ of ☐

Platinum

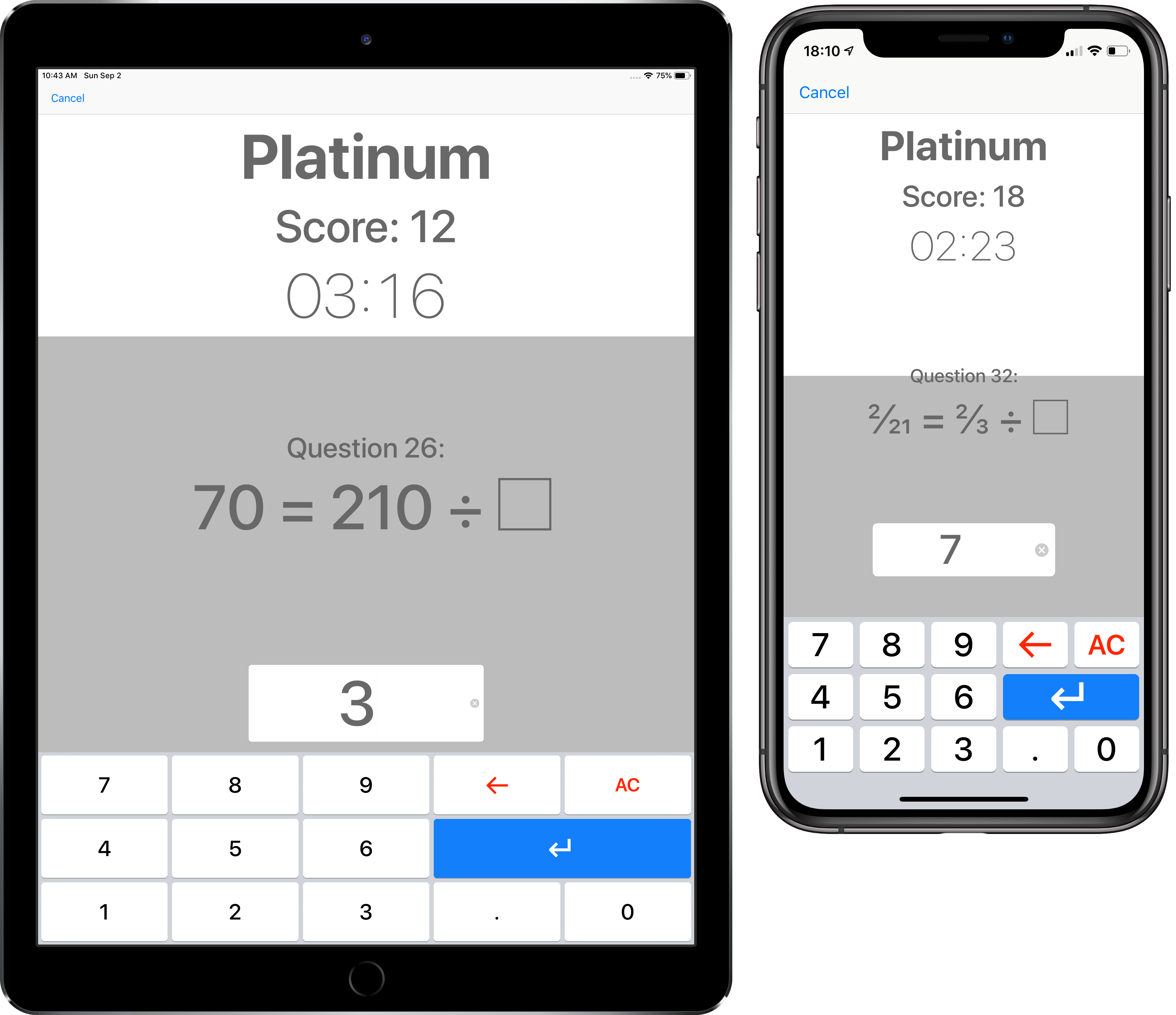
Many times tables tests would stop after practising up to the 12 times table, but in Platinum you will stretch your knowledge of all your tables to numbers in the tens column (for example 40 × 3 = 120), and the tenths column (for example 0.6 × 7 = 4.2).

You will also practise dividing fractions by a whole number, and turning mixed numbers into division questions.

Here are the new question types you will practise:

• Multiplying a number in the tens column by a whole number, learning that if one of the factors is ten times larger, then the answer is ten times larger too:
• 20 × 9 = ☐
• Multiplying a number in the tenths column by a whole number, learning that if one of the factors is ten times smaller, then the answer is ten times smaller too:
• 7 × 0.8 = ☐
• Missing whole number: which whole number do you multiply by to get the answer?
• 0.7 × ☐ = 2.8
• Missing number in the tens column: which number in the tens column do you need to multiply by to get the answer?
• 360 = 4 × ☐
• Missing number in the tenths column: which number in the tenths column do you need to multiply by to get the answer?
• 4.5 = 9 × ☐
• Dividing a number in the tens column by a number between 2 and 12:
• 420 ÷ 6 = ☐
• Dividing a number in the tenths column by a number between 2 and 12:
• 0.9 ÷ 3 = ☐
• Dividing fractions by a whole number, learning that you multiply the denominator:
• ⅒ = ⅕ ÷ ☐
• Turning mixed numbers into division questions, learning that division can be written as an improper fraction:
• 2 ¾ = ☐ ÷ 4

Kryptonite

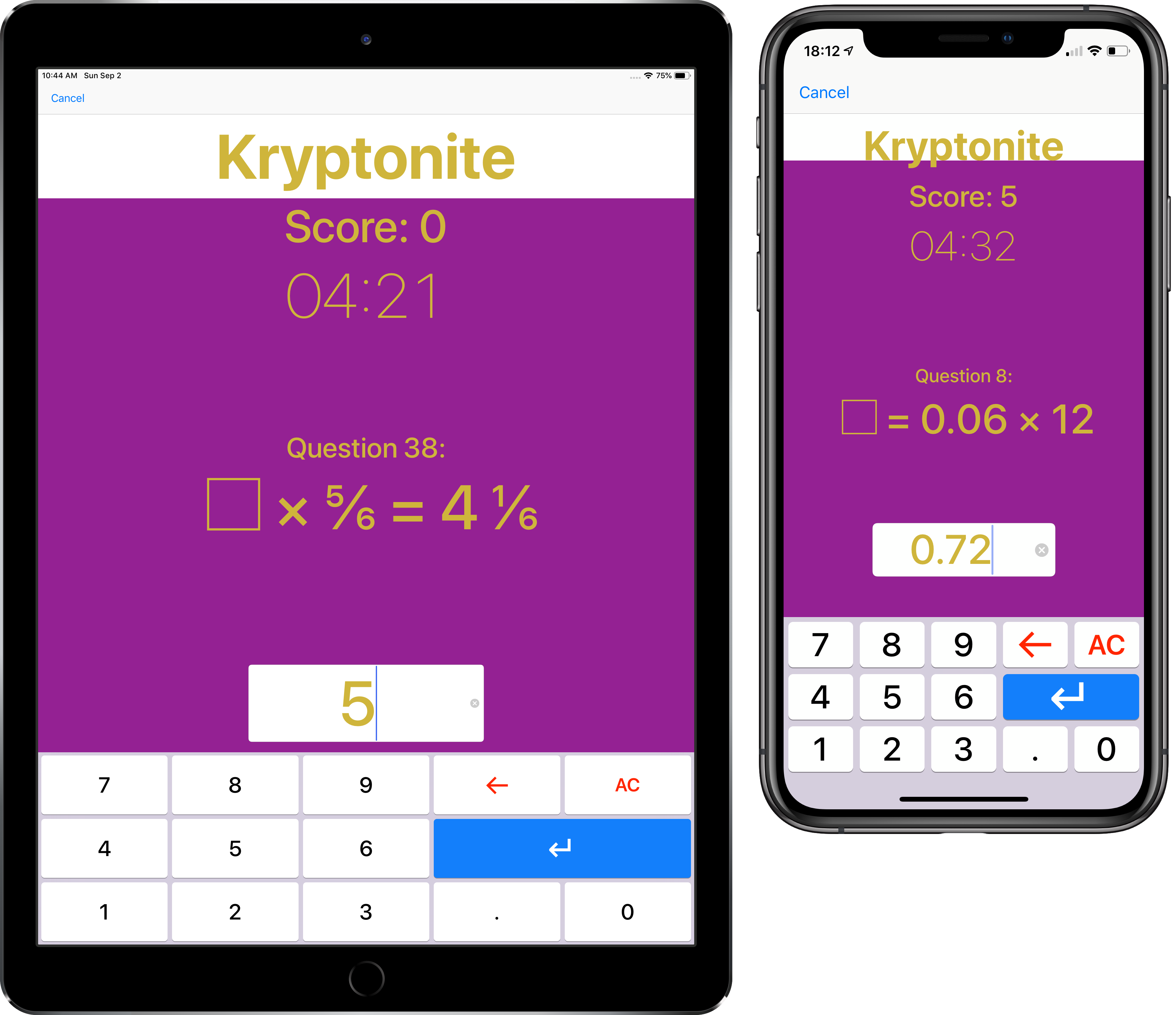
If you can regularly pass Kryptonite, then you will truly know your times tables back to front and inside out. In Kryptonite you will extend your knowledge of all your tables even further, into the KS3 Curriculum. The numbers you will work with will be in the tens and hundreds columns (for example 400 × 3 = 1200), and also the tenths and hundredths columns (for example (0.06 × 7 = 0.42).

You will also practise squaring and cubing numbers, and multiplying fractions.

Here are the new question types you will practise:

• Multiplying a number in the hundreds column by a whole number, learning that if one of the factors is a hundred times larger, then the answer is a hundred times larger too:
• 600 × 11 = ☐
• Multiplying a number in the hundredths column by a whole number, learning that if one of the factors is a hundred times smaller, then the answer is a hundred times smaller too:
• 5 × 0.03 = ☐
• Missing number in the tens column: which number do you multiply by to get the answer?
• ☐ × 40 = 800
• Missing number in the tenths column: which number do you multiply by to get the answer?
• ☐ × 110 = 88
• Dividing by a number in the tens column, learning that if you divide by a number that is ten times bigger, the answer is ten times smaller:
• 24 ÷ 80 = ☐
• Dividing by a number in the tenths column, learning that if you divide by a number that is ten times smaller, the answer is ten times bigger:
• 36 ÷ 0.9 = ☐
• Finding fractions of a number, when the numerator can be bigger than 1, learning that you divide by the denominator and multiply by the numerator. Also squaring and cubing numbers, learning that squaring and cubing is calculated before multiplication and division:
• ¾ of 8² = ☐
• Working out what to multiply a fraction by to get a mixed number as the answer, learning how to turn mixed numbers into improper fractions:
• ☐ × ⅘ = 2 ⅖